 |
|
|
|
WE-13C Transmitter Harmonic Power Output
|
|
|
Bob Brandenburg, M.S., TIGHAR #2286 |
| Introduction | ||||||||||||||||||||||||||
| This paper presents the estimated power output of the WE-13C transmitter at harmonic frequencies. | ||||||||||||||||||||||||||
| Background | ||||||||||||||||||||||||||
The final power amplifier of the WE-13C transmitter was a Class-C amplifier using 2 Western Electric type 282A tetrode (screen grid) vacuum tubes in parallel. The total (space) current in this type of amplifier flows in pulses of duration less than a half-cycle at the input (fundamental) frequency. The pulse duration is denoted by θ and is expressed in degrees. The space current pulse waveform has a direct-current (d-c) component, plus alternating current (a-c) components at the fundamental frequency and harmonics of the fundamental. The amplitudes of the components can be calculated by Fourier analysis. The WE-13C schematic diagram (Morgan, 1941) shows that the transmitter did not have harmonic suppression circuitry at its output. Hence harmonic current components present in the output would flow in the antenna, causing radiation at harmonics of the fundamental. |
||||||||||||||||||||||||||
| Methodology | ||||||||||||||||||||||||||
| Terman and Ferns (1934) showed that the space current in screen-grid tubes is proportional to (Eg + Esg/μsg)α, where Eg and Esg are the control grid and screen grid potentials respectively, μsg is the amplification factor, and the exponent α is 3/2. The paper presents curves, derived by Fourier analysis of the space current pulse waveform for α=1 and α=2, giving In/Im as a function of 0°≤θ≤180°, where Im is the space current, n = 0 denotes the d-c component, n=1 denotes the fundamental frequency component, n = 2 denotes the 2nd harmonic component, etc. The 2nd harmonic amplitude peaks at θ=120°, and higher order harmonics peak at lower values of θ, suggesting that 120° was the upper limit for θ in harmonic generators. The curves also show that 130 to 150° is the optimum range for a Class C amplifier. The prevailing design philosophy of the mid-1930s to mid-1940s (Terman, 1937 and 1947) held that θ=140° was reasonable compromise between a number of conflicting factors affecting efficiency and power output. This value of θ was used for the present analysis, but the resolution of the printed graphs was not sufficient for accurate interpolation for α=3/2. However, equation (1) (Terman and Roake, 1936) allows the computation of I1/Im for any value of α by numerical integration: 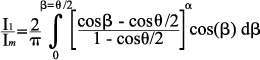 (1) (1) where β is the angular separation, in degrees, from the crest of the space current pulse. Equation (1) can be generalized for computation of In/Im by inserting “n” in the cosine term to the right of the expression in square brackets, where “n” is the order of the space current component, yielding:
Solutions of (2) for the present analysis were obtained by numerical integration using Simpson’s rule with enough points to ensure that the estimation error did not exceed one percent. The computed values of In/Im for θ=140° are:
Since the output power corresponding to a given a-c current component is directly proportional to the amplitude of the current component, the ratio of the output power at a given harmonic to the output power at the fundamental is given by In/I1 = (In/Im) / (I1/Im). The resultant power ratios for the 2nd through 5th harmonics are:
The output power at a given harmonic is the product of its power ratio and the WE-13C output power at the fundamental, which was 50 watts (Morgan, 1941). The resultant harmonic output power levels, in watts, for θ=140°, are:
The signal-to-noise ratios (SNRs) for cases involving harmonics in the post-loss-signals analysis were computed using these values for WE-13C power output at harmonics. |
||||||||||||||||||||||||||
| References | ||||||||||||||||||||||||||
| Morgan, H. K. 1941. Aircraft Radio
and Electrical Equipment, Second Edition. New York and Chicago: Pitman Publishing Corporation. Terman, F. E. and J. H. Ferns. 1934. “The Calculation of Class-C Amplifier and Harmonic Generator Performance of Screen-Grid and Similar Tubes,” Proc. I. R. E., Vol. 22, No. 3, March. Terman, F. E. And W. C. Roake. 1936. “Calculation and Design of Class-C Amplifiers,” Proc. I. R. E., Vol. 24, No. 4, April. Terman, F. E. 1937. Radio Engineering, Second Edition. New York and London: McGraw-Hill Book Company. Terman, F. E. 1947. Radio Engineering, Third Edition. New York and London: McGraw-Hill Book Company. |
||||||||||||||||||||||||||
|
||||||||||
|
|
||||||||||
|